Using Elemental Matrix to Obtain Inverse Matrix

이전에 역행렬의 특성과 기본 행렬에 대해 다루었다. 하지만 역행렬을 어떻게 구하는지는 다루지 않았다. 행렬식(determinant)을 이용하여 구하는 것이 일반적이지만, 그것은 나중에 다루어보도록 하고 이번에는 앞에서 다루었던 기본행렬을 이용하여 역행렬을 구하는 방법에 대해 알아보자.

 

그 전에, 아래 $(a) ~ (d)$를 살펴보자. 

▶ A가 $n \times n$ 행렬이라면, 다음의 문장들은 동일하다. 즉, 모두 참이거나 모두 거짓이다.

$(a) \; A$는 가역이다.

$(b) \; A\mathbf{x} = 0$는 오직 자명해만 갖는다.

$(c) \; A$의 rref는 $I_{n}$이다.

$(d) \; A$는 기본 행렬의 곱으로 표현 가능하다.

 

$(a)$를 통해 $(b)$를 증명할 수 있고, $(b)$를 통해 $(c)$를 증명할 수 있고, $(c)$를 통해 $(d)$를 증명할 수 있고, 다시 $(d)$를 통해 $(a)$를 증명할 수 있다.

 

$(a) \Rightarrow (b)$

$A$가 가역이고 $\mathbf{x_{0}}$를 $A\mathbf{x} = \mathbf{0}$의 어떤 해라고 생각하자. 양변에 $A^{-1}$을 곱하면

 

$(A^{-1}A) \mathbf{x_{0}} = A^{-1} \mathbf{0}$

 

따라서 $\mathbf{x_{0}} = \mathbf{0}$이고, 자명해만을 갖는다.

 

나머지에 대한 증명은 생략하겠다.

---

위의 $(d)$에서 행렬 $A$는 기본 행렬의 곱으로 표현 가능하다는 것을 보았다. 즉 아래와 같이 사용할 수 있는데,

 

 

$ A = E_{1}^{-1}E_{2}^{-1} \cdots E_{k}^{-1}I_{n} = E_{1}^{-1}E_{2}^{-1} \cdots E_{k}^{-1} $

 

이를 다시 $A^{-1}$꼴로 나타내면 아래와 같다는 것을 알 수 있다.

 

$ A^{-1} = E_{k} \cdots E_{2}E_{1}I_{n} $

 

즉, 단위 행렬 $I_{n}$에 특정 기본 행 연산을 취하면, A의 inverse를 구할 수 있다는 사실을 알 수 있다. 좀 더 엄밀하게 이야기해서, 가역행렬 $A$의 inverse를 찾기 위해서, $A$를 단위 행렬로 만드는 기본 행 연산의 sequence를 찾고, 그것을 다시 $I_{n}$에 대해 적용하면 $A^{-1}$를 얻을 수 있다는 사실이다. 

 

아래 예시를 보자.

 

$ A = \begin{bmatrix}
1 & 2 & 3 \\
2 & 5 & 3 \\
1 & 0 & 8 \\
\end{bmatrix} $

 

$A$가 다음과 같을 때, $[A | I]$ → $[I | A^{-1}]$로 바꾸는 과정을 통해 $A^{-1}$을 얻게 된다.

 

출처 - Elementary linear algebra 12th editon

 

출처 - Elementary linear algebra 12th editon

 

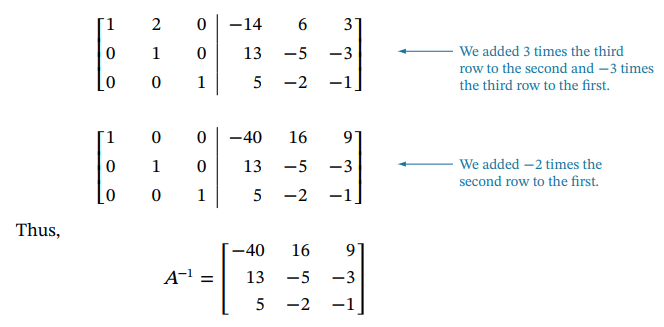
자세한 Logic은 위 예시를 따라가다보면 이해할 수 있을 것이다.

 

References

1. Elementary linear algebra 12th editon, Howard Anton, Anton Kaul